Answer:
We need to have M∩C and P∩C
as small as possible.
Then Need to keep only M∩P as high as possible = 5
Smallest possible number of students choosing chemistry = 18 + 2 = 20
The answer is, "20"
CAT Prep 2023 | CAT Previous Year Question Papers With Solution | CAT 2022 Student Review | PaGaLGuY
CAT 2020 Quant Question: Functions
If f(x) ≥ 0 for all real x, and g(20) = 72, then the smallest possible value of b is
A. 16
B. 1
C. 4
D. 0
Answer:
Value of b is at least 4
Hence, the answer is, "4"
CAT 2020 Quant Question: Speed, time & distance
The distance from B to C is thrice that from A to B. Two trains travel from A to C via B. The speed of train 2 is double that of train 1 while traveling from A to B and their speeds are interchanged while traveling from B to C. The ratio of the time taken by train 1 to that taken by train 2 in travelling from A to C is
A. 7:5
B. 4:1
C. 1:4
D. 5:7
Answer:
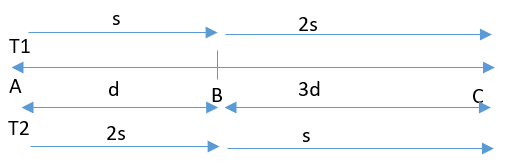
Trains be T1 and T2
and speed is s and 2s
Ratio of time taken for train 1 to train 2
5 : 7
The answer is, "5:7"
CAT 2020 Quant Question: Mensuration
The sum of perimeters of an equilateral triangle and a rectangle is 90 cm. The area, T, of the triangle and the area , R, of the rectangle, both in sq cm, satisfy the relationship 
. If the sides of the rectangle are in the ratio 1 : 3, then the length, in cm, of the longer side of the rectangle, is
A. 27
B. 18
C. 21
D. 24
Answer:
Sides of the rectangle are in the ratio 1 : 3
Take as x and 3x
Area of Rectangle = 
Take an equilateral triangle with side a
Area = 
Now from the options longer side 3x = 27
x = 9. Sides of the rectangle are 9 and 27.
If x = 9, Then a = 6
It works, hence longer side of rectangle is 27
The answer is, "27"
CAT 2020 Quant Question: Linear & quadratic equations
The number of integers that satisfy the equality 
A. 5
B. 4
C. 3
D. 2
Answer:
We can have three possibilities for the equality of form 
First n = 0, then x = 1 and then x = -1 and n = even 
Using first x = -1, and substituting in given equation
(Acceptable)
Using second condition, 
Solving x = 2 or x = 3 (Both are acceptable)
Last condition x2 -5x + 7 = -1
-5x + 8 = 0
No integer values,
So 3 values satisfy the equality
Hence, the answer is, "3"
CAT 2020 Quant Question: Linear & quadratic equations
In how many ways can a pair of integers (x , a) be chosen such that 
A. 7
B. 6
C. 4
D. 5
Answer:
In the above equation the value of constant cannot be more than 1
So |a – 2| = 0 or = 1
x = 0 or 2 or -2
For all these possibilities value of a = 2
|x| = 1
So, x = 1 or x = -1
Then |a – 2| = 1, a = 3 or a = 1
Four combinations of (x,a) are possible already we have 3
Totally 7 pairs
Hence, the answer is, "7"
CAT 2020 Quant Question: Races
Two circular tracks T1 and T2 of radii 100 m and 20 m, respectively touch at a point A. Starting from A at the same time, Ram and Rahim are walking on track T1 and track T2 at speeds 15 km/hr and 5 km/hr respectively. The number of full rounds that Ram will make before he meets Rahim again for the first time is
A. 5
B. 3
C. 4
D. 2
Answer:
R1 = 100m and R2 = 20m
Speed of Ram = 15km/hr and Rahim’s speed = 5km/hr
Time taken by Ram = 
Time taken by Rahim = 
Ratio of the time taken by Ram : Rahim = 5 : 3
After 15 units of time Ram and Rahim will be at starting point and meeting
That time ram would have done 3 rounds
The answer is, "3"
CAT 2020 Quant Question: Speed, time & distance
A and B are two points on a straight line. Ram runs from A to B while Rahim runs from B to A. After crossing each other, Ram and Rahim reach their destinations in one minutes and four minutes, respectively. If they start at the same time, then the ratio of Ram’s speed to Rahim’s speed is
A. 2
B. 2√2
C. √2
D. 
Answer:
t = 2
Ram takes 3 minutes and Rahim takes 6 minutes
So Ratio of Ram’s speed : Rahim’s speed= 2 : 1 = 2
The answer is, "2"
CAT 2020 Quant Question: Geometry
Let C1 and C2 be concentric circles such that the diameter of C1 is 2cm longer than that of C2. If a chord of C1 has length 6 cm and is a tangent to C2, then the diameter, in cm of C1 is
Answer:
The line from the center bisects chord of length 6
into 3 and 3. Since the triangle is of 3, r and r +1
Triplet of triangle 3,4 and 5
r = 4, r + 1 = 5 (radius of C1)
Diameter of C1 = 10
Hence, the answer is, " 10"
CAT 2020 Quant Question: Work & time
John takes twice as much time as Jack to finish a job. Jack and Jim together take one-thirds of the time to finish the job than John takes working alone. Moreover, in order to finish the job, John takes three days more than that taken by three of them working together. In how many days will Jim finish the job working alone?
Answer:
John = x units/day
Jack = 2x units/day
Jim = x units/day (1/3rd of John does = 3x units, out of which jack does 2x)
Total = 4x units/day
John’s time taken = x(n+3) = 4x × n
Then n = 1 day for 4x units
For x units, Jim will take 4 days
The answer is, " 4"
CAT 2020 Quant Question: Percentages
In May, John bought the same amount of rice and the same amount of wheat as he had bought in April, but spent 150 more due to the price increases of rice and wheat by 20% and 12%, respectively. If John had spent 450 on rice in April, then how much did he spend on wheat in May?
A. 590
B. 580
C. 560
D. 570